Satellite clocks
Well under 1 meter
Ephemeris error
Each satellite broadcasts ephemeris data that precisely describe its orbit
The ephemeris data can be used to plot the location of an SV in earth-centered, earth-fixed (ECEF) X,Y,Z coordinates
Why is it important to know its orbit?
Your GPS receiver estimates your position using the calculated pseudorange from an SV at an estimated position
Your receiver calculates the estimated position of an SV using:
The orbital elements for the specific SV and
The current time
The SV positions are given in earth centered, earth fixed X, Y, Z coordinates (ECEF XYZ)
Here is a link to a paper that describes ECEF XYZ and how to convert to other representations (author [email protected])
Here’s a description of Kai Borre's EASY Suite applications that use ECEF coordinates for satellite and receiver positions (Kai Borre, Inside GNSS)
I ported his MATLAB code to Javascript to calculate the SV orbits and derive the receiver position for the app in this course
The GPS control segment is in charge of updating each SV’s ephemeris on a regular basis (about every 2 hours)
Satellite orbits are attenuated by gravitational interactions with the earth and moon
The solar wind modifies the speed of an SV and hence its orbit
The solar wind is powerful enough to accelerate spacecraft
GPS ground stations (part of the control segment) monitor the positions of each SV over time and update each SV’s ephemeris
Less precise data on the position of all the SVs is also broadcast by each satellite—this is referred to as almanac data
Overall, ephemeris error contributes less than 1 meter of position error
Error due to receiver electronics
Various sources of noise, problems with signal acquisition (poor antennas), or computational power can lead to a range of error values for positions
Contributes 1 to 2 meters error
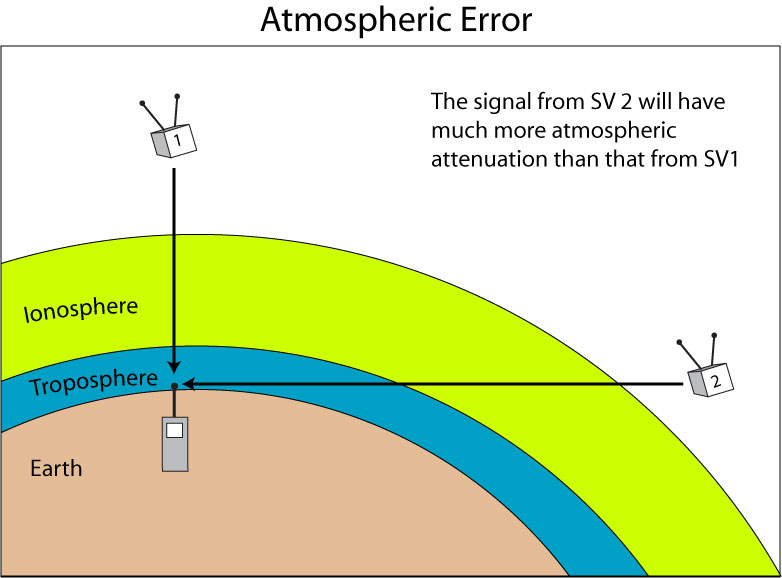
Atmospheric error
A GPS signal travels from an SV that is approximately 20,000,000 meters (12,600 miles, 20,000 km) above the surface of the earth
About 19,000,000 m is through near vacuum
The rest of the trip passes through varying atmospheric densities
Electromagnetic radiation changes speed when it crosses atmospheric boundaries
The ionosphere and troposphere account for the greatest speed variations
Ionospheric attenuation can be accounted for somewhat
Tropospheric attenuation is somewhat more random
The ‘wet’ region of the troposphere attenuates the signal the most
Since a signal from an SV that is low on the user’s horizon passes through a large part of the troposphere, better GPS units can ‘mask’ those SVs from contributing positional information
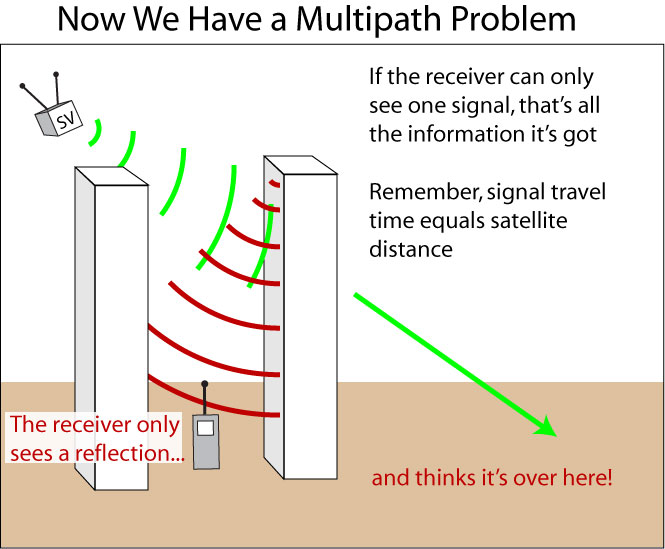
Multipath error
Multipath error is commonly encountered in FM radio broadcasts
If you’re sitting in traffic, your radio station can seem to ‘overlap’ with itself due to signal reflections off neighboring cars or buildings
If a modern receiver encounters 2 signals from the same source, it is usually programmed to ignore the signal that arrives ‘last’
If it only receives one signal, but that signal arrives as a reflection off a building or some other feature, significant positional error can occur
Here is an app that demonstrates multipath error
Green lines represent direct signal paths from the SV to one of 3 receivers on the ground
Orange lines show signals that have reflected off a wall before arriving at a receiver
An orange line travels further and takes longer to get to the receiver than the green line so its pseudorange (estimated distance to the SV) will be greater too
If a green line and an orange line both make it to the receiver, the receiver uses the signal having the shorter pseudorange (the one that arrived at the receiver first)—no harm done!
However, red lines show signals that only come to the receiver from a reflected path without an accompanying direct signal
Since the receiver doesn't get a direct signal, it take the pseudorange of the reflected signal as the actual distance to the SV—oops...
You can drag the SV back and forth across the scene to see the possibilities
Intentional error—Selective availability (SA)
Intentional error introduced into the coarse acquisition (CA) code through manipulation of SV clock data
Approximately 85 meters of error can be attributed to selective availability
SA was turned on when GPS went fully operational in 1993 but was turned off in 2000
SA can be corrected for by differential GPS techniques (more on this later)
That’s mainly why it was turned off in the first place!