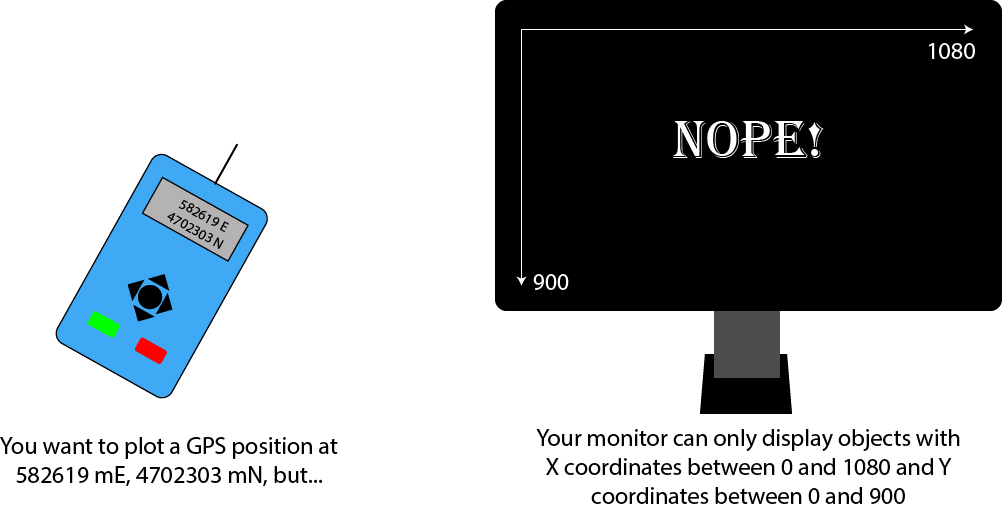
Normalizing Coordinates
Here is a very typical mapping problem:
Fortunately, there's an easy way to do this by transforming your data into normalized coordinates. Normalization is a way of transforming a quantity in an arbitrary range down to a narrow range, typically between 0 and 1 (or -1 to +1 if negative values are important). Normalization is just a scaling (zooming) transformation. So for our GPS problem, the process would look like this:
The Normalizing Coordinates app lets you create data in one coordinate system and display it another. You can move the origin of the digitizer choose whether or not to preserve the aspect ratio between the digitizer image and the monitor image. Aspect ratio is the relationship of the scales of the coordinate system axes to one another. If they share the same scale (the coordinate spacing is the same), then aspect ratio is preserved. If not, well, then it's not!
Using the App
Let's take a look at the app web-page:
For the moment, leave the origin at the center of the window. Make sure to uncheck Preserve aspect ratio. Click to add a node to the upper left of the origin. You should now see something like this in the digitizer and monitor windows:
In my case, I clicked at digitizer coordinate x = -122, y = -78. The copy of the node appears at monitor coordinates x = 98, y = 122. Very different numbers!
Now let's look at the calculations:
The digitizer and monitor widths are 'physical' values--they represent the full resolution of the input and display devices. Note that the digitizer is longer in width than height and the monitor is just the opposite. Also, the longest dimension of the digitizer (its width) is longer than either of the 2 monitor dimensions.
The X and Y values of the digitized node (the one you just created) are always given relative to the position of the origin. X is negative to the left of the origin and positive to the right. Y is negative above the origin and positive below. It's important to note that the position of the digitized point with respect to the digitizer window doesn't change if you move the origin--only the node's coordinates change. Regardless of the origin's position, if you subtract the minimum X value from the maximum, you will always get 700 (the width of the digitizer). Likewise, the difference of the min and max Y values will always be 400.
The values xNorm and yNorm are the normalized equivalents of the digitized node coordinates. If Preserve aspect ratio is unchecked, both will vary in the range 0.0 to 1.0. If it is checked, then only xNorm will vary between 0.0 and 1.1, yNorm will vary from 0.0 to a value less than 1.0.
xNorm and yNorm are just ratios of distances in X and Y from the left and top edges respectively. In my case, my xNorm value of .33 means that my digitized node at x = -122 is 33% of the total distance from the left edge of the digitizer to the right edge. yNorm = .31, is at 31% of the distance from the top to the bottom.
Having these ratio distances is key to the solution of mismatched coordinate systems. If we have nodes recorded as ratios, then we can multiply them by the dimensions of the target device to find suitable coordinates. If a node is 1/3 of the way across the width of one device, then we can put it 1/3 of the way across any device.
We calculate xNorm by finding the digitized node's distance from the the left side of the digitizer (-122 - -350 or 228) and divide that by the entire X coordinate range (350 - -350 or 700). We do the same thing for yNorm in terms of its digitized Y coord and the Y coordinate range.
Take a look at the calculations for xScaled and yScaled. These are the coordinates that our node will assume on the monitor. Multiplying xNorm by the width of the monitor gives us a coordinate on the monitor 33% across in X (at x = 98). Multiplying yNorm by the monitor's height gives us another coordinate in Y 31% of the distance from the top to the bottom (at y = 122).
What about the aspect ratio? So far, we have only been looking at computations that do not preserve it, meaning that digitized X values are always normalized with respect to the X range and Y to the Y range. Try drawing a square (as close as you can get) while not preserving aspect ratio. Here's what I got:
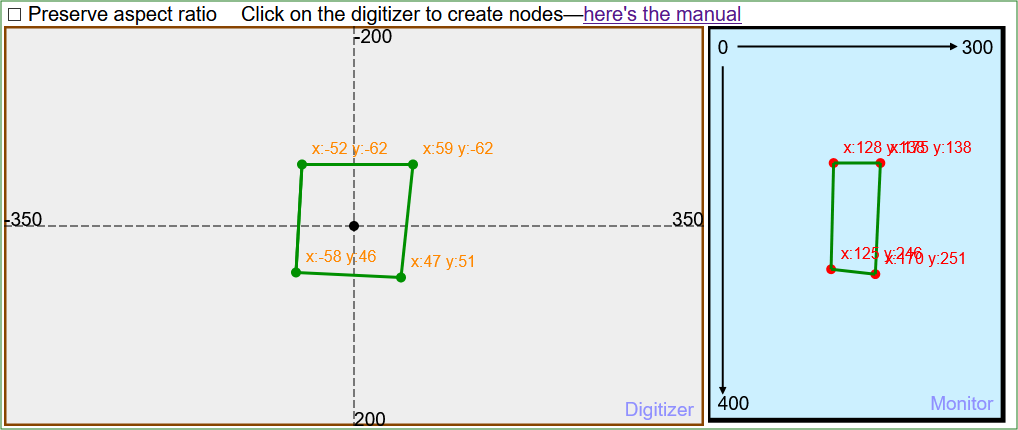
If we normalize our 2 axes to different ranges, the scale of the 2 axes are different. In this case, the X values on the monitor are scaled smaller than Y because the monitor width is smaller than the monitor height. Now check Preserve aspect ratio and look at your image. Here's mine:

How does this work? Simple--instead of normalizing X to the X coordinate range and Y to the Y coordinate range, we normalize them both to whichever range is greater. In this case, digitizer nodes' X and Y coordinates are both normalized to the width of the monitor (the X range). The points are scaled to the monitor by multiplying both xNorm and yNorm by the monitor's height (its Y range). That way, the shape you draw in the digitizer preserves its geometry on the monitor (although scaled smaller in both X and Y).
Things to try
Add more points to create polygons. Continue to click on the digitizer to make more nodes. Close the polygon by clicking back on the first node. It will yell at you if you cross lines or put points inside of existing polygons (I took much of this from another app I wrote to demo polygon topology).
Select any node to see its calculations. As you hold down the shift key, click on an existing node in the digitizer window. The node will turn yellow, the matching point on the monitor will also turn yellow, and the calculation data for the selected node appears.
Click, hold, and drag the origin to a new location. You will see that the coordinates of all the digitized nodes change with respect to the new origin position. Look at the xNorm and yNorm values for the selected node as you move the origin. Although the first lines of both equations change, the results do not. This is not a bug! Since the nodes themselves don't move, we are always going to get the same xNorm and yNorm ratios no matter where the origin happens to be.
Keep checking and unchecking Preserve aspect ratio to see how that affects the shape of your polygons and the calculations you see.
Things to think about
No individual piece of this app is terribly complicated--it just seems that way when all the computations are strung together. Good computer graphics apps are like good magic tricks. It takes a lot of work to make them but the results are cool.