Manual: The Simple Trig Functions App
This app shows you the relationships between Cartesian point coordinates and trigonometric functions. Although some of the assumptions it makes may seem unrealistic for real-world applications, that's actually not the case! Almost any computer graphics program uses the techniques that are demonstrated here. If you still remember your basic high school trigonometry you should have no problem using the app. If it's been a while, there are numerous websites that can help you out or just ask me--I'm happy to help.
Using the App
Take a look at the opening screen. You will see a large circle, superimposed on a pair of X and Y axes, with its origin at X = 0, Y = 0. The values of X increase positively to the right of the origin, and negatively to the left. Y increases negatively from the origin toward the top of the page, and positively to the bottom. On the right hand side (or below the circle on smaller screens) you will see a green frame displaying the calculations for each selected feature.
The coordinate system for the axes and the circle extend from -1.5 to +4.5 in both X and Y with the origin at the center. There is no special significance to this range except that it made it easier for me to create a unit circle (a circle with a radius of 1) in a space that is very easy for you to read without zooming in and out a lot.
Don't worry about units--they're not important! The results apply equally well to centimeters, meters, inches, miles, and so on.
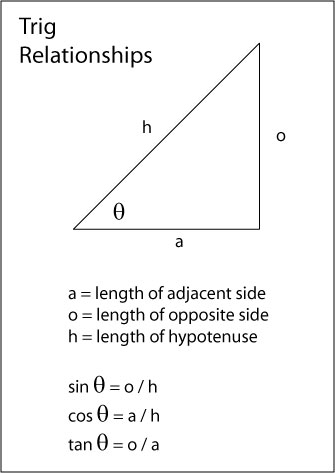
What are the basic trig functions? Sine, cosine, and tangent. These functions give the ratio of 2 sides of a right triangle that always occur for a given angle at one of the non-right angle vertices. For the angle θ (Greek lower-case theta) and sides a (adjacent), o (opposite), and h (hypotenuse), then
the sine of θ gives the ratio of the length of the opposite side of the triangle to the length of the hypotenuse, and
the cosine of θ gives the ratio of the length of the adjacent side of the triangle to the length of the hypotenuse.
These ratios hold for all right triangles. If you can find the ratio of 2 side lengths, you can look up the corresponding angle with the inverse (or arc) functions arccosine (cos-1), arcsine (sin-1), and arctangent (tan-1)
What is a unit circle? Very simply, a circle centered at the origin (X = 0, Y = 0) with a radius of 1, like this one:
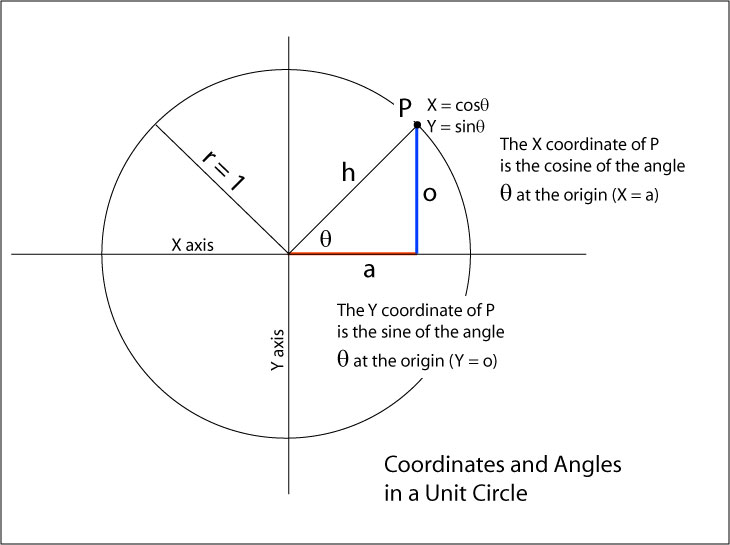
In the diagram above, point P is at coordinates X, Y. Since the circle's radius = 1, the hypotenuse (h) also equals 1. The length of side o is the y coordinate of point P and the length of side a is the X coordinate of point P. Since h = 1, the sine of θ is the length of the opposite side (o) divided by 1, or just Py. and the length of the adjacent side (a) is a / 1 or just Px.
What about tangent? As long as point P is not sitting on the origin, we can talk about the angle it makes with respect to the X or Y axis. The sine and cosine ratios always have a non-zero hypotenuse length in the denominator so they're always safe to compute. However, the tangent ratio is not always safe--when P is on the Y axis, a will be equal to 0. Dividing any number by 0 is undefined and cannot be computed. Avoid using tangents unless you are sure that you will never have a case where a = 0.

What about circles that have a radius greater than 1? No problem--just divide by the radius to get the sine or cosine value.
What about circles that are not centered on the origin? Next semester we'll look at affine transformations--functions that allow us to transform points in a coordinate system to give the affect of moving (translating), changing the size of (scaling), or changing the orientation of a point relative to its former location or orientation. This is a fundamental way of changing the viewer's point of view with respect to a map or any other type of graphic image. We'll see how to do this next semester but understanding how unit circles work makes it a lot easier to understand how affine transformations work.
Try out the app
Move points P and Q by clicking, holding, and dragging them around the circle. I have established the 0 radian (rad)/0 degree mark on the positive X axis and have angles increase in the counter-clockwise (CCW) direction around the circle.
The 0 mark and the direction of increasing angles is completely arbitrary--I could have picked the -Y axis and clockwise direction (as for compass bearings) if I wanted.
The following chart is a convenient roadmap for correspondences between radian and degree measures:
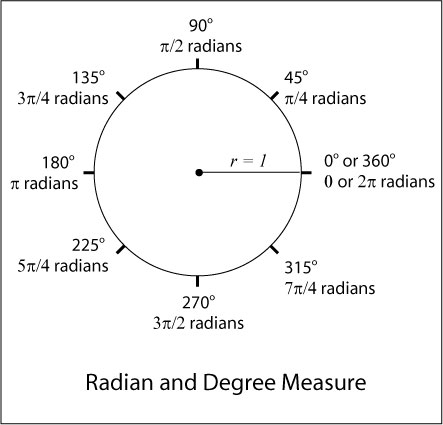
One nice thing about radian measure and unit circles: since the circumference of a circle is C = 2πr, if the radius is 1, then C = 2π. You can think of any portion of the circle in terms of sections of its circumference. So 90 degrees is 1/4 of a circle which equals 1/2 π radians, and so on.
When the app starts, you'll see point P on the X axis and Q at a 45 ̊ angle with respect to the X axis (select Degrees above the Radius slider). Both the X and Y coordinates of Q are 0.7071067811865474. Since the radius of the circle starts out at 1.0, the X and Y values provide the cosine and sine of the angle θ, either measured at the vertex at the center of the circle or as the arc from the 0 mark to point Q. Using a scientific calculator (either in Windows, or Mac, or your smart phone), taking the inverse sine of that number gives you .7854 radians (appx.) or 45 ̊ (exact). Your calculator should be able to display radian or degree measures.
Moving either point P or Q will show the calculations for that point in the green text box on the right (or below the graphic on smaller screens). All of the values except the X and Y coordinate values are shown with reduced precision to save space on the graphic. The internal floating point computations were done with 32 bit precision but, as you know, these are also approximate values (a digital computer cannot have infinite precision without infinite memory resources).
Clicking on PQ Arc calculations shows the angle between P and Q, measured counterclockwise starting at P. Since moving P or Q automatically resets this feature, you have to keep selecting it if you want the PQ angle (sorry!). I've created a special function, diff2piRange(), that makes it easy for me to display the angular difference between 2 points anywhere on the circle (not just in 1 quadrant).
What are the ranges for the trig functions? This can vary quite a bit between different math computational packages. I'm using Javascript trig functions in this app. Its cos-1 and sin-1 functions will only give you values between 0 and 90̊ which is a pain when you want to give angles over an entire circle. For that, most people use the atan2 function which is defined in most modern math packages (like Javascript). In the computations, the ±θ values are computed with cos-1 and sin-1 functions while the θ values were done using atan2.
Try changing the radius of the circle with the slider to see how that affects computations. Even though changes in the radius affect the X and Y coordinates of the circle, the cosines and sines (and the resulting angles) are not affected. Neat, huh? Hit 'Reset Radius' to set it back to 1.0.
A note on this implementation
All of the functions in this app can be written in virtually any modern programming language. Unfortunately, writing an app specifically for the web takes a lot of effort these days. At one time, The Java programming language, Adobe Flash, and Microsoft Silverlight were each capable of hosting interactive web apps all by themselves. Over time, each of these languages became more susceptible to hacking. At this moment (summer 2019), I'm using a combination of code written in HTML5, Javascript, CSS, and SVG (a graphics language). I don't expect you to create this kind of code yourself by the end of the semester but you are more than welcome to inspect the code (in Chrome, right click on the page and click View page source--other browsers have similar tools) or to ask any questions about it. One of the sites I use frequently to learn new things (which I do every day I program) is W3Schools.com. There are many others as well.
Remember, you are learning how to learn a programming language. Once you get it, learning another is much easier (and more fun) than the first!
Simple Trig Functions and Coordinate Data, copyright James Mower 2019



