![]()
Galton's Symmetric Studies of Stature (1886)
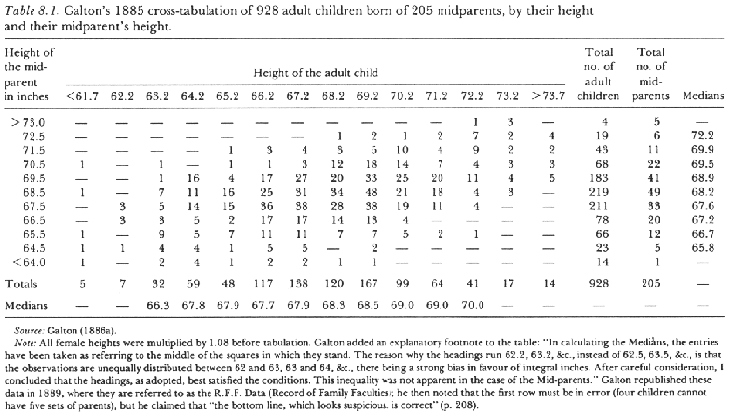
From quincunx and sweet peas, Galton proceeded to his studies on human heredity. In 1885 he analysed the "correlation" (without this concept yet, though) between children's heights and their parents's heights. He collected the data of 928 children (heights of adult children) and their parents. However, unlike sweet peas, a human child has two parents. Galton treated this problem by introducing the notion of "midparent": the average of the father's height and the mother's height, the latter scaled up by 1.08. Likewise, all feamale heights were multiplied by 1.08, which is obtained by comparison of the average male height and the average female height. Thus Galton obtained the following table which is a cross-tabulation of 928 children and 205 midparents.
�@
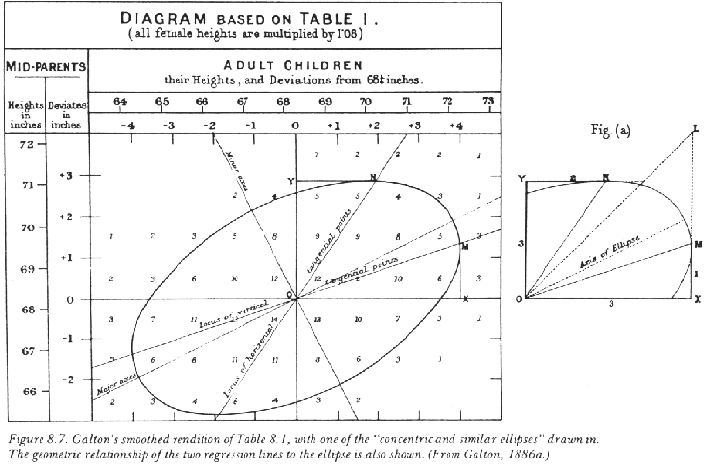
This table suggested many interesting points. Each row and each colum, arranged according to heights, can be regarded as showing a mini-normal-curve (conditional on the given height)! And since the heights of children and those of midparents are treated symmetrically, you can see "reversion" on each side; i.e. the reversion on the side of children with respect to midparents, and the reversion on the side of midparents with respect to children. Thus it is clear that reversion has nothing to do with heredity! Further, Galton noticed another interesting feature by giving a smooth rendering of the table (a la meteorological diagram) by connecting the same values of the data in the table. Look at the following diagram.
�@
�@
To Galton's surprise, he obtained a series of concentric and similar ellipses (one of which is shown in the diagram); moreoever, by drawing a tangential line (to any ellipse) perpendicular to the vertical axe you obtain the average reversion ratio of child (upon midparent), and by drawing a tangential line perpendicular to the horizontal line you obtain the average reversion ratio of midparent (upon child), and this fact is shown in the righthand side figure. He asked mathematician J.D.Hamilton Dickson for help in order to clarify the matter mathematically.
Dickson derived Galton's ellipses and their interrelationships, using only analytic geometry and the laws of probability. ... Dickson's result held as a general relationship between any two appropriate variables, not only those linked by heredity. The coefficient of reversion [reversion ratio] was thus independent of heredity; it was purely a property of statistical manipulation itself. (Kevles 1986, 16)
The preceding "symmetry" eventually led Galton to the discovery of important concept of "correlation". For a more detailed description and analysis, see Stigler (1986), 283-290.
Last modified October 28, 1999. (c) Soshichi Uchii
�@